“Every election is a sort of advance auction in stolen goods”- H.L. Mencken
It is unfortunate that most of us are confronted by thieves only when they have a significant advantage. Although that advantage may take the form of a weapon, or superior brute force, most often it is one of position. Poker, ever the great equalizer, compels us to tolerate the grand larceny of an aggressive button from our vantage in the blinds. Yet it provides one situation in particular whereby an unwise thief may find his ill-gotten gains slip through his fingers. Let us wade into the Battle of the Blinds!
Defending our big blind against a small blind steal with deep stacks is the most structurally advantageous pre-flop situation in Pot-Limit Omaha. The fact that our pre-flop call is guaranteed to close the action elevates this set-up over a button versus loose cut-off set-up. It is curious then that a very large number of players open a very wide range from the small blind when the action is folded around to them. In this article we are going to take some first steps towards an ‘optimal’ big blind defending strategy against a given small blind opening range.
Hard Parameters
Intellectual laziness abounds even among ‘strong’ poker players when discussing the impact of mathematical insights on poker strategy. “It depends…” is all too often a diversionary gambit that provides our interlocutor with a facade of wisdom. If, “it depends…” is not followed by an explanation of the series of circumstances upon which the insight does indeed depend, then our interlocutor could have saved us time and money by admitting to his ignorance
When the BB faces a raise from the SB his opponent is risking 2.5BB to win a 1.5BB pot with a pot-sized raise (or 1.5BB to win 1.5BB with a min-raise). We immediately identify ‘BB fold to SB Steal’ as a hard parameter2; if we fold more than 50% to a min-raise or 62.5% to a pot-sized raise our opponent may raise any 4 cards profitably. Thus this number alone informs us as to the minimum width we must defend to an SB steal as part of an optimal strategy. Of course in practice, unless our response is to 3-bet our entire range, our opponent will see a flop sometimes with any hand he opens with. Accordingly, even if he plays nit-or-fold (say only continuing with top two+, a wrap, or a flush draw) he will still win a fraction of every pot. Tabulated below is the frequency with which our opponent will flop {Top two+, Wrap, FD} when called after raising with a given range fraction.
| Range Fraction (HU rankings) | Top two+, Wrap, FD |
| 27% | |
| 35%-40% | 26% |
| 45%-50% | 25% |
| 55%-60% | 23.5% |
| 65%-70% | 23% |
| 75%-80% | 23% |
| 85%-90% | 22% |
| 95%-100% | 20% |
You will notice that even the very worst hands flop something playable at least 1/5th of the time. If we take the extremely conservative estimate that our opponents lose the entire pot 4/5 of the time when we call and retain half the pot 1/5 of the time when we call, we see that their EV when we call is 0.2*0.5 – 0.8*2.5= -1.9bb when they pot-size raise pre-flop. If we never 3-bet then we must defend at least 45% of the time to prevent our opponent potting any four cards pre-flop. A similar calculation yields a minimum of 58% defensive width versus a min-raise. Note that few players are as incompetent as assumed in the above calculation post-flop, and so these numbers represent an absolute floor to our defensive range. Any decision to defend tighter than this against a given player is an exploitative adjustment to that player’s tighter opening range. This is because our opponent could deviate unilaterally to opening any four cards to exploit us when we fold with a higher frequency than calculated.
Soft Parameters
Now we have ascertained the minimum width we must defend from the BB we turn our eyes to the more difficult task of deciding just how wide to defend. One of the ‘soft parameters’ we can use is the equity for a given fraction of our range against our opponent’s total range. The reason this is so valuable is that as ranges widen we are no longer as concerned with polarization potential as we are when tight. Mediocre two pair will commonly get to show down in position BB versus SB. Furthermore, most 6max players are very poor at playing wide ranges out of position post-flop. This soft parameter is tabulated in the heat map below:
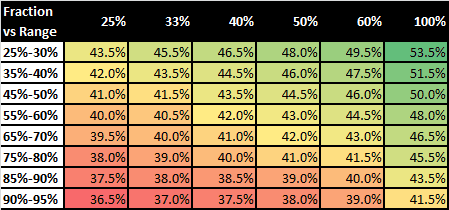
Heat Map displaying equity for a given BB range fraction versus a SB opening range.
The reader will naturally use other ‘soft parameters’ to determine his pre-flop decision, not least his post-flop edge in both single-raised and 3-bet pots, his opponent’s fold to 3-bet and his opponent’s 4-bet range3. However, the value of the heat map displayed above should not be underestimated. You may use it to improve your consistency in hand evaluation. If you are happy defending a 59th percentile hand against a 40% open from a given player, then you should be happy to defend a 79th percentile hand against a 60% open from a similar player. If there is ‘no way’ you would defend a 79th percentile hand against a 50% open, you should be cautious defending a 49th percentile hand against a 25% open.
To conclude, I will provide the reader with a few equity reference points against a 25% opening range:
AJ92:Axx is in the 35th percentile and has 43.5% equity
JJ95ss is in the 11th percentile and has 46.5% equity
KQ96ss is in the 27th percentile and has 43.5% equity
T874ds is in the 47th percentile and has 43% equity
I would consider all of these hands playable from the BB versus a 25% SB steal despite the fact that I would fold most of them were I on the button facing the same opening range. Closing the action for a discounted price is a fine option, and I would encourage you to take that option whenever you can.
Blind play is the absolute best starting point for practicing innovative post-flop play. You are typically in position against a wide range and have no fear of being squeezed pre-flop. If the reader is looking to be more aggressive but is unsure where to start then this is the place to spew a little with creative lines. I would also like to extend my thanks to those readers who have recently translated articles on my blog into Russian and Japanese. Expect to see some exciting developments on this site in April.
Good luck at the tables,
Quad

Hey Quad,
I have a somewhat related question.
Specifically, the effects of preflop card removal. The easiest way to explain it is through an example- if it folds to you in the SB in a 9-handed PLO game and you’re thinking of raising, the chance that the BB has a top 15% hand has to be significantly higher than 15%, right? Since over half the deck is already folded away and the muck is heavily weighted towards low cards because we assume no one mucked any decent KKxx+, BBBB, etc.?
I guess my question is, just how high is the chance that BB has a top15% hand? I’m horrible at math, but if I were to take a completely random guess, I’d guess if it folds to you in SB at a “standard” 9-handed table and you have a hand like 8765ds, the chance that BB has a top15% is probably over 30%.
Thoughts? Hope this was good food for thought for you as well. I’ve read every post and love your blog.
Hi Don,
Thanks for your question, it is indeed an interesting one.
At first glance, your intuition would seem quite promising. For instance, if we take the first 8 opponents to require an Ace in their hand to open, the probability that the 9th player is in the top 15% of starting hands does indeed double to around 30%. Unfortunately, the probability that at least one of the first 8 has an Ace in his hand is over 98%, and so this is a pretty implausible hand constraint for those 8 players. It is only under such a loose hand constraint that your intuition actually holds.
If we go one step further, and assume that none of the first 8 players has a hand in the top 15%, then the probability that the 9th player has a hand in the top 15% rises to a mere 17.5%. This is so small a rise as to be inconsequential in your pre-flop decision making 100BB deep.
Naturally our model is rather crude, we could in fact assume that the CO/BT have much wider requirements than a top 15% hand, but the addition of two players who have 4 cards each insufficient to open does not affect the mathematics much.
In fact, the place where your intuition would be most relevant would be in an MTT situation at very low stacks. So in a PLO turbo with an average stack size of around 10BB you could expect many of the first 8 players to be shoving any Ace. Under such a circumstance you could conceivably consider implied card removal as a factor in the width of your SB push.
I think that answers your question,
Quad
Hey Quad,
Thanks! Great answer.
If we take the extremely conservative estimate that our opponents lose the entire pot 4/5 of the time when we call and retain half the pot 1/5 of the time when we call, we see that their EV when we call is 0.2*0.5 – 0.8*2.5= -1.9bb when they pot-size raise pre-flop.
why is the half pot 0.5 in the calculation?
when you calculate the flop%, you add up the filtered numbers? like here: top two+, flushes (top two+ taken away) and straight draws( 9-12,13-16,17+)?
great article as always, keep them coming 🙂
Hi Di,
Thanks for your comment: it’s prompted me to mention two important things.
The first, in answer to your question, is that if the pot is 6BB post-flop and our opponent will expect to retain, on average, 3BB of that pot, then he makes a 0.5BB profit from his initial investment of 2.5BB.
The second is to remind the reader of the premise under which these calculations are taken: We set out our hard parameter as preventing the SB strategy of opening any four cards from being +EV. However, from the SB’s perspective, he just has to do better than -0.5BB to make raising better than open-folding. I did not use this as the threshold in the article, since non-zero thresholds tend to disorient people without a lot of mathematical experience. However, if the reader is working through these calculations from that premise, he will find that the BB must continue even wider than the article states.
In my opinion, in the present games, most BBs are way too tight (especially with calling widths, they often try to compensate for weak positional play by 3-betting most of their continuing range) and most SBs correctly exploit that by opening wider (but way too wide theoretically). Unfortunately, those same SBs persist with aggression too much post-flop against the BBs tighter range: hence the present artificial equilibrium with many regular’s SB/BB strategies.
Hope that shed some light on why this spot is so interesting,
Quad
“if we fold more than 50% to a min-raise or 37.5% to a pot-sized raise our opponent may raise any 4 cards profitably.”
Shouldn’t the 2nd percentage be 62.5?
Dear Peter,
Yes, thanks for pointing that out I have made the correction. My train of thought for this article was on how wide we must defend and, in the case of the min-raise, the defend/fold to figures are symmetric with respect to the change in SB/BB perspective. The later calculations remain correct.
Thanks again,
Quad
inputting the hands {AJ92:Axx, JJ95$ds, KQ96$ss, T874$ds} into Range Explorer yields the same figures as you mentioned above for VR. Why did I not need to adjust for a 25% range somewhere? and why don’t we use the 6H instead?
Thank you for articles, i’m working through PLO theory everyday and I’m hoping to be able to contribute one day
Regards
Daz
okay nevermind, I’m understanding now… thanks again
Hello Quad,
How do you get the percentile of specific hands?
Thanks
Hi pacmang,
I’ve been using Odds Oracle’s ‘%VR’ for Heads-up rankings. See the link in the sidebar for the ProPokerTools website.
Quad