“There is nothing so terrible as activity without insight.”
– Johann Wolfgang von Goethe
There’s no escaping it- from a purely financial standpoint poker is a negative sum game. This simple fact presents a conundrum that every mainstream poker training business tries very hard to ignore: It is impossible to have as a sincere mission the objective to ‘teach the world to play great poker’.
“Teach the world to play great poker” – the reader may laugh at loud at the very idea of it. Yet the absurdity of this phrase belies the seriousness of a structural problem that pervades the poker training industry: There is an inevitable conflict of interest that arises between expanding the customer base of a training site and the benefit derived from that training site by each individual customer. In this way, the very success of a poker training site punishes its customers!
In this article I am going to introduce a metastrategic concept that is essential to the success of your poker career- the value of strategic information. After reading the article you will understand why so many players resent mainstream poker training sites for cannibalizing the games, and how to estimate the value of emerging opportunities in poker. You will also discover why a different approach to strategic information distinguishes Cardquant from mainstream poker training sites.
Of necessity this article will only appeal to a fraction of my readership, but those are the very people that I am most eager to make a connection with. So if you really enjoy this article, and want to see the next article in the series come along shortly, please take the time to introduce yourself in the comments. Let’s get started…
This article is the first in the Cardquant Identity Series– a series in which I will introduce a number of new concepts to my readership, explain how they relate to my work at Cardquant, and how my work at Cardquant relates to my larger vision for my scientific research and my philosophical writing.
Information Distribution Curves
It is well established that poker games are games of incomplete information. What is seldom explicitly stated, much less formalized, is that each variant of poker has its own associated information distribution among the competing population, and that this distribution has a strong deterministic influence on the distribution of profits from that game variant.
I have developed the ‘Information Distribution Curve’ as a visual way to represent the various structural features that determine the value of information in a game variant.
Let’s take a look at an example of an Information distribution curve for a poker variant in order to familiarize the reader with the key features of such curves.
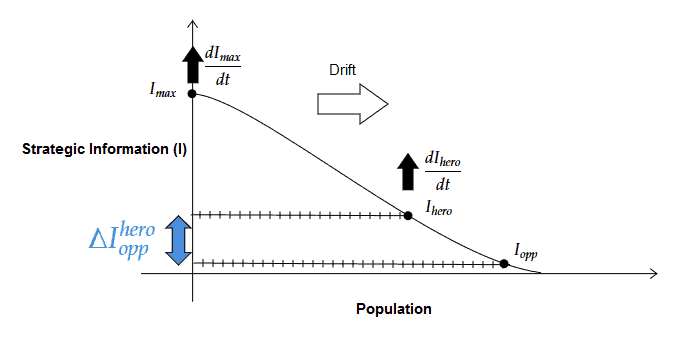
The curve shown ranks the population in order of the level of strategic information about the game that they retain at a given moment in time. The ‘x’ axis spans the population, terminating at the 100th percentile. The ‘y’ axis indicates the quantity of information that each player retains, as a fraction of the theoretical perfect strategic understanding. Whether this perfect understanding is attainable, or is in fact some form of infinity for any given variant, is a philosophical digression that is not significant for the discussion at hand.
I have marked out three key points on this curve:
- Imax :- This indicates the participant who has the highest level of strategic information for the game variant.
- Ihero:- This point represents you, the hero, indicating your current level of strategic information for a game variant in the context of the wider population.
- Iopp:- This point indicates the level of strategic information for a single opponent on the curve. Any point on the curve which is not you represents a potential opponent.
The double-headed blue arrow indicates ∆I: the difference in information level between you and a given opponent, with a positive value giving you the advantage and a negative value conferring an advantage to your opponent. In a heads-up game, only one ∆I would be relevant but in a 6-handed cash game, or a multiplayer tournament, the level of strategic information for every one of your opponents in the game matters (although each opponent’s level is not equally weighted- another complication).
The information landscape for any given game variant will develop over time. Each single-headed arrow on the curve indicates a feature that will change across time:
- The black vertical arrow adjacent to Imax indicates the rate of discovery dImax/dt of strategic information at the leading edge of the game variant.
- The black vertical arrow adjacent to Ihero indicates the rate dIhero/dt at which you, the hero, learns new strategic information. That similar such arrows could be drawn for every one of your opponents follows trivially.
- The white horizontal arrow on the curve indicates the ‘information drift’, which is a term I have coined to describe the rate at which the high level information accessible to those at the top of the population flows to those lower down in the population. For now a qualitative description will suffice, although there are some natural ways to formalize information drift which I will briefly discuss below.
Before we continue there is one other essential feature common to all game variants that I have not indicated on the diagram above- the information ceiling. The information ceiling is the theoretical limit to which it is possible to formalize any particular game variant. The reason that tic-tac-toe is not played for money, and in fact rarely even played at all other than with children, is because the information ceiling is so low that perfect strategy is accessible to all people with even a basic capacity for reason.
Now that we know how to read an Information Distribution Curve it’s time to explore some ways in which you can use the Information Distibution Curve concept to make better metastrategic decisions in your poker career.
Metastrategic Applications of Information Distribution Curves
I’m going to write a formal definition and more thorough discussion of metastrategy in a later article in this series, but for now think of metastrategy as the analysis of the structural factors that determine what the real (as opposed to the ludic) rules and payoffs are in a game, and consequently whether a game is worth playing.
I can assert unequivocally that your metastrategic decisions are the most important ones that you will make in your poker career because the relationship between metastrategy and strategy is hierarchical, with the former dominating the latter.
For any given poker variant it is desirable to be at as high a level of ‘I’ as is possible.
This fact should be obvious, and is generally well understood by all those players who seek to improve their game by studying training materials, or attempting to research it themselves. From this observation it follows that the value of playing in a particular game (as distinguished from the value of the game variant generally) is strongly determined by the difference in I (∆Iho1,o2…on) between you and your opponents.
In an ‘open-borders’ online poker world the set of opponents that you face will have values of ‘I’ that are representative of the population for that game variant. Factors such as the stakes that you play, the time of day that you play, and whether you play on weekends or in holiday seasons will affect which subset of the population you face for a given session, but the accessibility of such online games ensures that the Information Distribution Curve dominates the value derivable from a given game variant.
A poker game variant is said to be ‘information saturated’ when there is very little difference between the level of strategic information available to the top of the population compared with that available to the bottom. The information distribution curve for such a game is shown below:
The Limit Holdem Information Distribution Curve
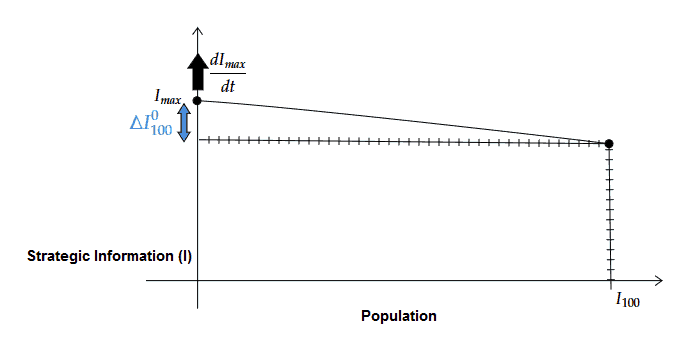
This game variant is information saturated because the difference ∆I0100 between the very strongest and the very weakest players participating in the variant is too small for even the best players to maintain a high win-rate. Without a large influx of new fish, or a profound conceptual breakthrough that raises the information ceiling or an acceleration of the rate of development at the leading edge dImax/dt, then there is little profit in the open-source game.
The information distribution curve above I understand to be an accurate representation of the current state of Limit Holdem as we move into the year 2020.
It is clear that there is very little profit to be made playing open-borders games in an information saturated game variant. A clear understanding of the concepts introduced so far enables one to see that the most profitable opportunities in poker will be found in either closed games, in game variants with a high information ceiling, or in game variants with a low information drift. Since these three identifiable game properties are not mutually exclusive it follows that the most lucrative poker games will combine all of them.
I will briefly discuss each property in turn below:
Closed games
Closed games are those where access is restricted based on criteria determined by the game’s gatekeeper. In closed games it is possible for you to have a ∆Iheroo1,o2…on that is far more favourable than those available in open-borders games drawn from the same game variant. Examples of such games are any and all home games, many live games spread in casinos, and the emerging app-via-agent game. It is important to understand that if the main reason that a particular game is highly profitable is because it is closed, then that game will either be difficult to get access to, involve an unusually high level of risk (ranging from illegal underground games to unregulated games to unscrupulous opponents), or both.
It behooves me to mention the perpetual metastrategic aspect here- which is that is generally desirable to be perceived as having a lower level of I than your real I in order to participate in lucrative closed games. The advantage of having a real I far higher than your perceived I only changes at the point where your perceived I is so high that very wealthy people actively want to play against you because of your status as a brilliant player.
Game variants with a high information ceiling
The concept of an information ceiling helps to explain a feature critical to the longevity of Poker as a family of game variants in general- which is the birth of new and complex variants.
A game variant with a low information ceiling permits even professionals with moderate talent to learn enough to reliably crush purely recreational players.
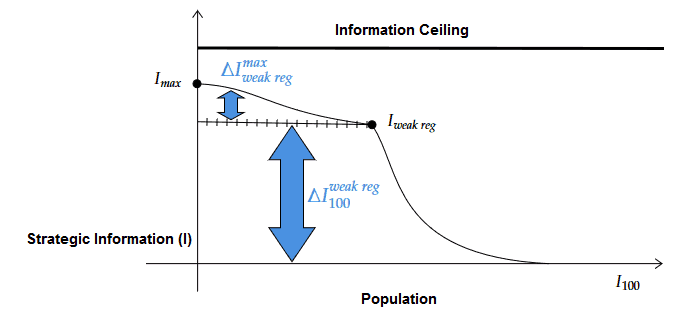
On the information distribution curve above we see that a low information ceiling results quickly in a small ∆Imaxweak reg and a large ∆Iweak reg100.
Once the recreational players that provide the capital for profitable games believe that a large fraction of their opponents have too great an information edge in one game variant they will switch to another. We have seen this first with player migration from No Limit Holdem to Pot Limit Omaha, more recently with the rise of Short Deck Holdem, and now 5 Card PLO is emerging as a variant where recreational players perceive the information edge to be low. It is not a coincidence that the Cardquant Research Institute does work on the three more contemporary games and that it has done comparatively little work on either No Limit Holdem cash games or Limit Holdem.
In games with a high information ceiling it takes a longer time for the game to be so well understood strategically that a large body of serious players can systematically beat recreational players. It is common for mediocre professional players to attribute to variance those downswings which in reality are due to their limited understanding of a complex game.
Game variants with low information drift
The long-term value of a poker variant is strongly determined by Information Drift, and this long-term value in turn determines the value of a high level of I in that variant- the faster the information drift, the less time one has to exploit a high level of strategic information.
This is where things start to get murky, because the perceived Information Drift does not have to match the real Information Drift. In a poker variant where there is little to no training material widely available, the real Information Drift is self-evidently low. But the real Information Drift can also be low in a game where there is a lot of training material available that contains little real strategic information and is mostly predicated on falsehoods. In such games, where the perceived Information Drift is high, players who have access to high levels of strategic information gain a huge edge, due to the excessive confidence of their opponents in weak strategy.
The Mainstream Poker Training Model: Information as a Commodity
The reason that most poker players hate the existence of mainstream poker training sites, despite simultaneously paying for the material at a number of them, is because the mainstream poker training business model accelerates the real Information Drift for any game where its hired analysts are sufficiently competent to produce accurate work.
I have received a number of well-intentioned emails over the years from readers who have encouraged me to join a mainstream coaching site to ‘boost my profile’. Whilst such discussions have taken place in the past, the reason that I have never reached an agreement with a mainstream coaching site is the fundamental difference in philosophy. The Cardquant institute is driven by research over and above raw sales numbers and this research is intended for an elite few, not for the wider poker community.
Take a look at the Information Distribution Curve below to see the difference in function between the Cardquant Poker Strategy Research Institute and Mainstream Poker Training sites.
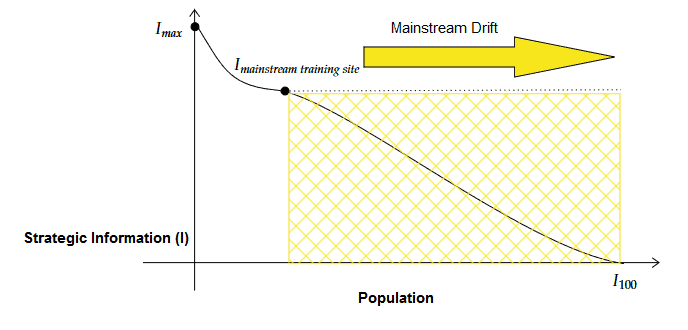
The mainstream poker training site model is inherently incentivised to maximize the reach of its training material, and to do so effectively it has to accelerate the information drift for any game variant that it touches. The larger the fraction of the playing population that purchase the courses, the greater the revenue of the site.
Mainstream poker training sites thrive on the commodification of knowledge- at the cost of the profitability and lifetime of any game variant which they sell material for.
There is also a natural antagonism between Creative Forces and the people who profit from turning information into a commodity. High level original work in a complex domain demands time and energy and for the researcher to be immersed in the creative process. In the current culture, the most widely-known authority on a topic is not the highest authority on that topic, because the person who is widely known is dedicating his time and energy to being popular rather than developing original ideas.
What do you think the most well-known poker trainers are better at, self-promotion or original research?
Cardquant is not built on a mainstream poker training business model, and the last section in this essay will show where my work here fits on an Information Distribution Curve.
The Cardquant Model: Sustaining Creative Research
Cardquant is a research-driven institution, which means that the activity here is directed towards pushing the frontiers of knowledge, developing new concepts and new technology, and consolidating the research into something that can be taught to others.
The information distribution curve below is a visual aid to understanding how I, as founder and research director, protect my work and my private clients to sustain future research. (In doing so I am arguably executing a meta-metastrategy for those amused by such things!)
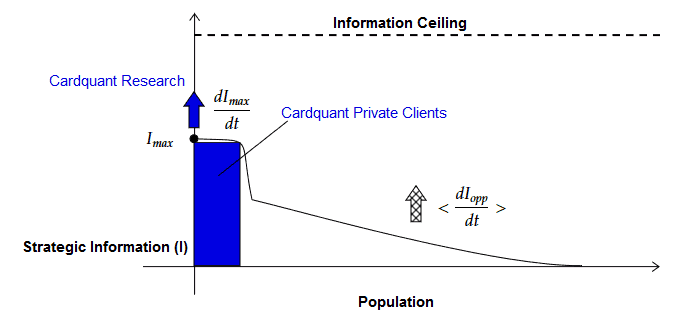
I work on new and complex games because they offer a high information ceiling which, as we have discussed, increases the long-term potential value of research in such a game. I ensure that the work that I do on any given game is at the leading edge so that I am at the Imax point for those games and, crucially so that the differential between dImax/dt (the rate of progress of research at Cardquant) and <dIopp/dt> (the average rate of progress of the general population) is high. This differential in strategic progress increases the potential value of research into the game.
If the barrier to Imax level research is low then there is less value in conducting research into that game. This is another reason why I have done little work on NL Holdem cash games, where so much is readily accessible to any analyst with commercially available software tools.
You will notice that I have been careful to emphasize the potential value of research above. It is an inherent structural feature of this approach that realising the potential value of research relies on sharing it with a small number of players who can maximally profit from it.
Early on in the life of Cardquant I was naive enough to believe that if I did great research and taught it very well to my clients, then that would be enough for my institute to succeed. Unfortunately a number of my highest profile clients did not want me to publish their glowing testimonials despite continuing to work with me as they told me point blank, “I don’t want my opponents to work with you.” Many of my clients ran coaching stables of their own (or more) and so I was in a strange position where many players were learning my ideas… but not from me.
These clients’ decisions were rational as they aimed to maximize their return on investment by limiting the Information Drift from me to their opponents. I am extremely grateful to my clients, past and present, for supporting my work over the years, and they have behaved with great integrity- almost without exception. As I grew to understand my clients’ incentives better and as I observed developments in the mainstream poker training industry I recognized the need for a better formal structure to protect the value of the research that I was creating, for both me and my clients.
For the last two years any new private coaching client of mine has signed an Intellectual Property protection contract before we start work together. This is a mutually beneficial arrangement where the incentives for all parties are aligned. The inevitable information drift to the population outside of my client base is reduced and my clients can enjoy an advantage with the strategic information that I teach them for a far longer period than if I shared the work immediately through a mainstream coaching model.
Given the model that I have described thus far the reader might well ask, “Why do you sell any poker training courses at all when your institute is so focused on discovering, developing and protecting new strategic information?”
A simple answer to that question is that, as information drift changes the landscape of a given game variant, the value shifts from the uniqueness of the information itself to how that information is formalized, organized, and communicated. A more complex answer is that strategic information is not synonymous with knowledge and that knowledge is more than just data. I will expand on these, and other ideas in the next article in this series- on Knowledge Organization.
The Cardquant Identity series continues with a discussion of Knowledge Organization in part 2…
If the ideas discussed in this article seem obvious to you in hindsight, then take a moment to reflect on your current behaviour. How much time are you allocating to watching strategy videos that are publicly available and how much time are you allocating to gaining access to closed games or studying strategic information that is restricted access? If you enjoyed this piece and have any clarifying questions then please share your thoughts in the comments below.


Great article. Very insightful. Really love the comment about meta strategic decisions being the most important decisions we make in our poker careers
Kudos to the work that has been done here! I’ll be following the journey, 😉
I found you by searching about 5 card PLO. As someone with mathematical-Game Theoric-Probabilistic-Statistical knowledge and understanding, I always find the amount of inaccuracy in poker articles and training materials absurd. Your article on 5 card plo was an exception, so I read more card quant articles, and more, and more….and I watched your 4 free videos on YouTube and I am going to analyze them again and again….every free material that you have (I would sign up for 5 card plo strategy research at cardquant as soon as I have the the high stake bankroll and money to invest, which unfortunately I think it will take at least one year)
At first, I felt unfair and sad, why is not your work more famous and appreciated. As a successful ex-Math Olympiad Teacher I have tasted the bitter reality that the real best content is not the one that get the most applaud.
After reading this article (Which I loved its title and was surprised by your amazing scientific modelling approach) I think its actually a good thing for me that your content is not the most applauded (yet your content might be the most appreciated by those who have the right mindset about poker) and I should be happy that I am one of the few poker players who understand the difference of your work with other training materials…(its not even about superiority of your material….its matter of meeting the necessities of real good poker training content)
Thank you very much for this, Keep up the great work
Really cool article, Phil!
I’ve felt for a long time that paying for a mainstream poker training site is only worth it those few times a year when some new trend emerges among regs and hearing the reasoning behind the move in a video from the source of the trickle-down, can save you a few dollars compared to calling down / overfolding vs the new trend in your regular games and paying for the experience at the table. There are a few instructors/videos that have taught me a lot (I miss CTS) but those are far and few between.
Anyway, you’ve convinced me it’s time to start learning a new game, or charm my way into some fishy, closed game. I just wish my desk chair weren’t so darn comfortable.
I detected Cardquant cause im struggling beating PLO5 online,my new passion after Corona forced me to quit Livegames, at least for the moment.
I just tried the free material (blog,videos,articles),which is already quite sophisticated, and which is an eye-opener that im not as good as i thought.
Im seriously thingking joining the Poker Training here.
When is part 2 coming?
Great article Phil, as usual.
As a 15 year online cash gamer, I’ve always felt the same way about the “mainstream” Poker sites. They don’t help you to get to the top, not even close. You just stay close to the average competition. To get to the top, you need to find your “own unique way”, and this will hold true for any profession.
You explained all of that in a logic and simple way, as you usually do. Great work!
Anxious for the next series =)
I have been a long time Phil’s costumer and even though I am familiar with his work, its not a surprise to me when he comes with such great insights such as this article. Your methods and the depth you approach the research on the game is one of the main reasons I rather review many times your videos and our coaching sessions together than to consume “commodities” as you put it. And even though I always approached my studies like this, you made it very clear in this article why I did it.
Looking forward to the next article.
Very insightful article, love it.
Thanks a lot
Hey Phil, Nicely written.
“strategic information is not synonymous with knowledge”
I think this is really true, say the average information out there in training sites is Ix, the average users of training sites will still have a much lower I than Ix because they cant turn that information into knowledge. I know I also struggle with that.
You mention short deck and 5 card PLO in the article. Would be interesting to hear your thoughts on the information gap in 6-max PLO online today. I personally feel the gap is still pretty huge for small stakes. Not too sure about mid and high stakes.
Would also like to hear your ideas on application of information, which I have a feeling you are going to talk about anyway. Poker have such huge mix strategies in all spots it is really hard to get a good grasp on how to apply what we learn form solvers.
-Kit
Thanks You for your efforts
As a 20 year veteran of live and online poker, I am always interested in strategic long term planning. The games have changed so much over the years and will continue to do so.
I’m predominantly a live NLH cash player, and I’ve spent money on Crush Live Poker (unsystematic but Ok) and Upswing (good for formulating a baseline to combat good regs).
The online poker I’ve played in recent years has been micro stakes NL and PLO. I played online NLH as a learning exercise to implement the baseline mentioned above. PLO definitely is something that I would like to spend more time on, and I did subscribe to Poker Math 2020, which I enjoyed and helped me win fairly consistently at PLO50.
Any way, I won’t ramble on further. Just wanted you to know that there are people out here reading, enjoying and learning from your output.
Keep it coming!